EDISON ACOUSTIC RECORDING
CONTACT : COMMENTS AND QUESTIONS
back/home
The following work comes from the study of many hundreds of Edison patents.
These were published by the staff at Rutgers University, New Jersey.
I am forever grateful to them for allowing me the opportunity to look into Edison's world -
surprising in its scope, ingenuity, and intuitive insight.
There is a great deal of information about the recording artists, but surprisingly little
about the equipment used to record them.
Without the engineers they would be sitting in the dark singing to themselves, or
at least, to a much restricted audience.
This part of the website is an attempt to restore the balance - even if only in a small way.
Example of an Edison Hill and Dale Disc Recording Disc01
Click on the title to
play:-
Pretty Lips
Where Do You Work-a John?
Electrical engineers use a lot of jargon, but it is jargon with a precise meaning.
This had not developed in Edison's time, so that it is necessary to start on the patents by
learning a new vocabulary.
For instance:
a transformer is an inductorium:
a matching transformer is a power amplifying inductorium :
a low frequency is a grave tone :
an electrical cutting head is a telegraphic recorder :
horn resonances are funnel tones :
mechanical resonance is sympathetic vibration :
non linear distortion is aberration and so on.
Example of an Edison Hill and Dale Disc Recording Disc02
Click on the title to
play:-
Somebody Loves Me
Tea for Two
The development of acoustic recorders is particularly interesting.
(a) It was the first time engineers struck the problem of producing a transmission path for
an audio signal with sufficient quality for entertainment purposes, so that the conditions necessary
for satisfactory transmission had to be figured out; and this had to run in parallel with the
design process.
(b) The dynamics of the acoustic recording and reproducing systems were almost certainly
the most difficult engineers had encountered up to that time.
The acoustic power gathered by a normal size horn in a recording studio varies between
about 1 microwatt and 1 milliwatt.
The conflicting requirements between sensitivity and good dynamic response led to
severe constraints and much compromise in the design.
The Basic Laws of Acoustic Recording
----------------------------------
A horn loaded diaphragm in an acoustic reproducer requires a constant velocity drive
for a flat response.
That is, the amplitude of the displacement of the drive must be inversely
proportional to frequency or, to put it another way, the displacement of the track
cut onto the disc must be the integral of the pressure wave in the studio.
This occurs when the velocity of the signal cut into the track is proportional to the pressure
in the sound wave.
Let the vertical track cut on the disc be given by:-
y(t) = Do + ΔD sin(ωt) where:-
y(t) is depth of cut: Do is the unmodulated depth and ω is the radian frequency
of the test cut.
Then:
v(t) = dy(t)/dt = ΔD ω cos(ωt) -- where v(t) is the velocity of the track.
vmax = ΔD ω
so ΔD = vmax/ω
If vmax is independent of frequency, then the track amplitude must be inversely
proportional to frequency.
The only mechanical systems in which velocity is proportional to force or pressure are
those constrained by viscous forces.
The key to acoustic recording may now be stated:
If viscous forces predominate over inertial and elastic forces in the acoustic recording head,
there can be no resonances and, further, the record will be cut with the correct dynamics for
reproduction by a horn loaded acoustic reproducer.
Example of an Edison Hill and Dale Disc Recording Disc03
Click on the title to
play:-
Alice Blue Gown
Irene
It is interesting to trace Edison's discovery of these concepts:-
He first mentions velocity in an 1888 patent application [393,966 4 Dec. 1888].
He notes that a click is produced in headphones only when the battery is connected
or disconnected, that is, when the diaphragm is moving.
Curiously, this seems to be the only patent in which Edison is totally on the wrong track.
The dynamics of acoustic recording were not understood, with a consequence that the high frequency
response of the system was poor.
To quote Edison:-
"All phonographs heretofore made have been unsatisfactory in the respect that they lacked
clearness and loudness of articulation."
In other words, no high frequency response.
His proposal in this patent is to offset the recording stylus from the vertical to produce
horrendous scanning distortion on play back, and so artificially increase the harmonic content
(and hence the apparent brightness) of the reproduced signal.
This is exactly the same mechanism of distortion found in a variable area optical
track with a scanning slit offset from the correct position:
which is at right angles to the direction of film travel.
To reduce scanning distortion in variable area recording, two monophonic tracks of half
deviation were placed side by side. The distortion was reduced with the deviation, but the output
was about the same as a single track.
The method proposed for the generation of scanning distortion is shown opposite.
The recording stylus was hinged, so that the movement was no longer at right angles
to the record surface, but had a component in the direction of the track velocity.
This is characteristic of all mechanisms of scanning distortion.
Efectively, the stylus position moves backwards and forward along the track with the recorded signal.
It would not be long before Edison discovered the necessity for linearity in the signal
path and the deleterious (aberration) effect of non-linear cutting forces in vertical recording.
[ 964,221 8 Jan. 1907 ]
Example of an Edison Hill and Dale Disc Recording Disc04
Click on the title to
play:-
Lonesome Mama Blues
Frolic of The Coons
By 1903 Edison had virtually solved the acoustic cutting head problem.
The solution is contained in two key patents:
[962,081 13 Nov. 1903] and [943,664 18 Nov. 1903]
All steady forces were removed from the recording diaphragm with the use of a tracker ball and
thrust reed.
The tracker ball was highly polished, so that it supported and positioned the cutting head
by gliding over the uncut material before the cutting head.
The depth of cut could be adjusted by varying the height of the tracker ball support
with a screw thread.
The edges of the diaphragm were not clamped in order to suppress free modes of vibration,
but were floated and sealed with burnt rubber. This was possible because there was no net force on
the recording diaphragm because of the tracker ball support.
Burnt rubber also provided damping or viscous control.
Viscous damping was further increased by slicing the diaphragm and thrust reed into sections
separated by the goop from burnt rubber.
Over ten thousand materials were tried as damping material. Burnt rubber was only material to have
the required viscosity and surface tension.
Burnt rubber is obtained by burning a stick of rubber while striking it on a plate. The "goop"
left on te plate is the required material.
Since all recorders were acoustic in this early period, Edison did not use the
term "acoustic recorder" but "burnt rubber recorder".
Example of an Edison Hill and Dale Disc Recording Disc05
Click on the title to
play:-
Chick, Chick, Chick, Chicken
Show That Fellow The Door
The general view of an early Edison acoustic tracker ball recorder is shown below.
Another view of the recorder is shown on the right.
The following points should be noted:-
[1] Vertical recorders permit much more favourable geometry than lateral recorders.
The shaft between the centre of the recording diaphragm and the cutting stylus can be made
very short and of low mass.
In a lateral recorder a pivot and cantilever must be used to get the required lateral deviation
of the stylus. This greatly complicates and degrades the response.
[2] Edison cutting styli act like a plough and meet the recording blank material "head on".
In disc recording Edison cutting heads therefore appear to be on the "wrong" side of
the turntable.
[3] The horizontal component of the cutting force is supported by the thrust reed (7) and (8).
Since this deflects vertically with the signal, it adds to the stiffness of the
recording diaphragm.
To increase the damping both the recording diaphragm and the thrust reed are sectioned
and the sectioned pieces separated by burnt rubber.
Example of an Edison Hill and Dale Disc Recording Disc06
Click on the title to
play:-
Measly Blues
Bass Ale Blues
|
|
|
|
A more detailed view of the vertical recorder. |
A close up view of the recording diaphragm and thrust reed. |
A close up of the edge support of the diaphragm. |
If we assume the motion of the recording diaphragm is uniform, and that it does not vibrate in higher modes, we can develop a very simple differential equation for its motion which, none the less, yields valuable insight into the conditions for good acoustic recording.
If x(t) is the track displacement, and v(t) is the signal velocity, we have :-
Example of an Edison Hill and Dale Disc Recording Disc07
Click on the title to
play:-
Love Bound
Dreaming of a Castle in The Air
Although the 1903 patents seem to a be a complete solution to the viscous
control problem, other methods of achieving the conditions derived in the above
equations were also patented.
Four of them are presented below:-
Lumped Damping
|
|
|
Here the viscous force can be increased almost without limit
with the use of a dashpot. |
Here the viscous material is lumped rather than
being distributed. |
Low Mass and High Compliance
|
|
|
Here the mass is decreased and the compliance raised. |
This employs the low density and high internal damping of cork. |
Example of an Edison Hill and Dale Disc Recording Disc08
Click on the title to
play:-
On The Oregon Trail
Little Peach
The only groove shape appropriate to vertical ( hill and dale ) recording is
the segment of a circle.
Edison realised this very early in the development of recording and patented
the groove shape on 17 June 1890 Pat: 430278.
In vertical recording with full modulation, the bottom of the groove can reach
the surface.
To maintain contact, the reproducing stylus must sit on the bottom of the groove.
A spherical reproducing stylus with a diameter smaller than the cutting stylus
will track a fully modulated groove.
Note that the problem of "groove fit" does not exist in Edison vertical recording.
The diameter of the spherical reproducing stylus can be reduced until the surface pressure
induced by the large forces encountered in acoustic reproducers starts to cause unacceptable
disc wear.
It is remarkable that Edison had considered the problem of tracing distortion
before 1900, and even more remarkable that he had invented and patented
a solution - the cylindrical stylus by 1899.
If a sphere traces a sinusoidal curve , the boundary condition is that the two
surfaces be tangental. The result is that the locus of the centre of the sphere is NOT
sinusoidal. This is called tracing distortion.
For very short recorded wavelengths there will come a time when the sphere
will no longer fit the hill and dale waveform at all.
An extract from the Edison patent describing this is shown opposite.
The language is formal and stilted but, nevertheless, the meaning is clear.
Tracing distortion can be reduced by decreasing the width of stylus contact
in the groove direction.
This reduces the contact area and increases the stylus pressure.
To recover more area the stylus must be extended across the groove.
In lateral recording the result is the elliptical stylus.
Long before the elliptical stylus, in fact by 1899, Edison had the solution for
vertical cut discs - the cylindrical reproducing stylus.
The appropriate patent is shown opposite.
If the edge of a cylinder is used as a stylus the above conditions are fulfilled.
Fig.2 is the plan of a track cut with an Edison circular cutter.
Fig.3 is a side view of a hill and dale track scanned with a spherical stylus.
Fig.4 is the same view, but with a cylindrical stylus.
Fig.5 is a ( somewhat exaggerated ) comparison of a cylindrical and spherical stylus.
With modern light weight high compliance pickups, the stylus diameter can be decreased
to a point where tracing distortion disappears. This is a valuable property of
vertical recording.
I use a 1 thou. spherical stylus at a weight of 1.5 grams. Unlike all my lateral 78s,
no tracing distortion is evident on the end of the Edison tracks.
The shape of the reproduced waveform when the spherical stylus is travelling over
a "hill" is different from when it traversing the bottom of a "dale".
The tracing distortion from a vertical cut disc shows asymmetry.
On the other hand, left and right deviations in a lateral track produce the
same distortion. The tracing distortion in lateral recording is therefore symmetrical.
The classical paper on tracing distortion is:-
A Theory of Tracing Distortion in Sound Reproduction from Phonograph Records
by W.D. Lewis and F.V. Hunt
The Journal of The Acoustical Society of America pp 348 - 365 1941
Now asymmetry produces even order distortion and symmetry produces odd order
distortion.
It is not surprising, then, that second order harmonic distortion in vertical recording
came out of the above analysis. The first distortion component in lateral recording
was third harmonic. This seemed to give vertical recording a bad name and interest was lost.
This is a pity.
Vertical recording has a lot of desirable characteristics such as: longer playing time:
freedom from retracking on overcutting: no problems with stylus fit.
Example of an Edison Hill and Dale Disc Recording Disc09
Click on the title to
play:-
King Tut
Barney Google
The dominant component of the cutting force decelerates the swarf to zero velocity.
We can now calculate this force:-
∫TF(t)dt = ΔI
where ∫TF(t)dt is the impulse provided by the cutting stylus.
ΔI is the change in momentum of material cut from the disc.
Since the cutting force is constant and equal to F we can write:-
∫TF(t)dt = F T
where T is the total time to cut the swarf.
If A is the area of cutter facing the track, and VT is the track velocity
then the volume V of track cut is:-
V = A VT T
If the swarf has a density ρ then the total mass ΔM brought
to a halt is given by:-
ΔM = V ρ = A VT T ρ
And the total change in momentum ΔI is given by:-
ΔI = A VT T ρ VT
= A T ρ [VT]2
Equating this to the impulse, we have:-
F T = A T ρ [VT]2 or:-
F = A ρ [VT]2
Now this is the force normal to the vertical. When the stylus moves vertically with signal,
a vertical component of force appears in phase with the vertical movement.
The stylus will cut into the disc at an angle Θ to give a vertical component
FV where:-
FV = F tan(Θ)
= A ρ [VT]2 tan(Θ)
If VS is the vertical signal velocity of the stylus then:-
tan(Θ) = VS/VT so:-
FV = A ρ [VT]2 [ VS/VT ] or:-
FV = A ρ VT VS
The cutting force is proportional to signal velocity, so it is viscous in nature
and will contribute to the system damping.
The constant of viscosity increases with the density and speed of the master.
Note: Edison recommends masters made from water soluble soap rather han wax.
Wax develops electrostatic charge from the friction of cutting and the
swarf clumps.
Soap is conductive and avoids this effect.
Edison particularly recommends Pears soap in the production of masters.[790,351 Feb.11 1903 ]
let us examine the equation for the cutting force derived above:-
FV = A ρ VT VS
In lateral recording the track area A is constant, so the cutting force, FV,
is viscous in nature and linear.
In vertical recording the track area A must vary with signal, and so the the cutting force
is always non-linear.
If the cutting force forms a significant part of the damping in the recording head, distortion
( or in Edison's language aberration ) will result.
If the recording stylus has a rectangular shape, then the variation of A with depth will
be linear.
Even in this case the cutting force will be non-linear.
The condition is inherent in vertical recording.
In Edison discs the track cross section is the chord of a circle, so the variation
of area with depth is highly non-linear - making the situation even worse.
If x is the depth of cut of a circular recording stylus of radius R, then a bit of
elementary geometry shows the area A of the track to be given by:-
A = R2{ cos-1( 1 - x/R ) -
( 1 - x/R )( 2x/R - (x/R)2 )1/2 }
This function is obviously far from linear.
Edison was well aware of non-linear cutting forces and their associated distortion
by 1907.
Early Edison vertical recorders used a recording stylus with a diameter
of 40 thou.
Edison realised that the large diameter had two disadvantages:-
[1] The tracks cut with the 40 thou. stylus were very wide - limiting
the recording time.
[2] The track area, and with it the cutting force, is large.
This is illustrated in patent 964,221 shown opposite.
A cross section of the tracks and a plot of the cutting force for the two
diameters is shown opposite.
Although both are non-linear, the 10 thou. stylus has the lower force and is therefore
preferable.
The 10 thou. diameter cutting stylus was standardised for discs.
The reproducing stylus diameter was about 7 thou.
This was a compromise between tracing distortion and bearing pressure on the disc.
The average groove depth was about 0.8 thou.
The solution Edison proposed in a further patent was low level recording.
This greatly reduces the distortion.
According to Edison it also had another advantage.
Low level recording allowed the use of a very short horn - so short that the horn
resonant frequencies ( funnel tones ) could be above the highest recorded frequency.
It is easy to check Edison's plots of cutting force with a digital computer.
The results are shown on the right and are the same as Edison's.
If the cutting force for the 10thou. diameter recording stylus is a small
fraction of the total viscous force, then the introduced non-linearity would be very low,
since the departure of the curve from linearity is not all that great.
A plot of track width and length along the track surface versus depth of cut
is given above.
The track width determines the cut depth for any given groove spacing.
The track length determines the area subject to shear force in the cutting process.
It turns out that, with the normal material used for masters - wax or soap,
this force is small compared to the inertial force.
In lateral recording on acetates this is probably not so.
Since the curve is reasonably linear in the centre, the variation in track
width gives a fairly undistorted view of the information contained in the
variable depth cut.
From the curves, it is seen that a groove cut with a 10.5 thou. diameter cutter
occupies all the land between the grooves of a 150 groove per inch spaced disc
when the cut depth is 1.2 thou.
The average unmodulated depth, then, should be 0.6 thou. if the grooves
are not to interfere at maximum recording level.
In vertical recording slight groove interference is no problem.
Groove skipping does not happen and there is usually no mutual
interference of the signal.
Wall thickness separating the grooves is decreased, leading to the possibility of
breakdown with a large reproducing stylus force.
Cylinders or discs recorded at a low level may have had little distortion ,
but were of no use on an acoustic reproducer.
Amplification to increase the amplitude of the track deviation was required.
Edison proposed to do this by lever action at slow speed.
It is not known if this system was ever used. Noise problems are not discussed.
A very similar system was used to transfer tracks between discs and cylinders.
Cylinder speeds were 120, 160, or 240 RPM. The disc speed of 80 RPM allowed
for simple gearing.
Drawings of the amplifier for cylinders are shown below.
Example of an Edison Hill and Dale Disc Recording Disc10
Click on the title to
play:-
The Old Grey Mare
How's Your Folks and My Folks
Edison described an electrical cutting head in his patent for a recording
telephone message machine. [ 1,012,250 Sept.15 1905 ]
The messages were recorded on a cylinder whose surface was shaved to erase the message.
Since the signal for the electric cutting head arrived over a telephone or telegraph line
it was called " a telegraphic recorder. " The name was used universally after this.
In 1913 an electrical cutting head was again mentioned to record the sound track for film
on a large diameter cylinder. [1,286,259 6 March 1913 ] .
It is not known if any of these devices were ever built, but they probably couldn't compete
with the fidelity purely acoustic recording had reached at that time.
As outlined in the WE4A section, Bell engineers had developed electrical recording by 1925.
An approach based firmly on mathematics had finally won out over Edison's intuition.
Edison was loath to adopt the new technique. He had spent a lifetime developing acoustic
recording to a high degree of perfection as evidenced by the included tracks.
It was his baby.
Some of the objections raised by Edison to electrical recording had some validity.
Valve amplifiers incorrectly adjusted were capable of producing horrendous distortion.
(aberretion ). The adjustment process before a recording session was tedious and required
trained personel in the then arcane art of vacuum tube amplification.
The reason for this is clear. The only tubes available at that time were triodes with
filamentary cathodes ( eg. The Western Electric 239-A and 205-D ), so cathode bias was impossible.
The bias on each tube had to be set individually from batteries - which then had to be maintained.
Against that the acoustic recorder was a self contained unit requiring no external
power source.
Acoustic recording could not compete with the sensitivity and frequency range of
the electrical system, and by 1927 elctrical recording was universal.
A photo of the electrical recording head for "Diamond Discs" is shown above.
It appears to have the same moving iron drive as the Bell cutter, but is much simpler
dynamically. It could well be a lateral cutter modified for hill and dale.
A turnover frequency has to be set for the end of constant velocity recording and the start
of constant amplitude to prevent excessive excursions at low frequencies.
I can find no published data on this for Edison electrics and chose 250Hz. -
the same as laterals. Subsequent listening tests seem to verify this.
In spite of the simplicity of the recording head compared with the Harrison cutter,
I find many of the Edison electricals very impressive.
Example of an Edison Hill and Dale Disc Recording Disc11
Note:Electrical Recording
Click on the title to
play:-
That Wonderful Night and You
Little Mother
A computer program to get a "feel" for how the various parameters in an acoustic
recorder interact is now described.
It is not claimed that the program is highly accurate, but it does give a good intuitive
insight into the dynamics of an acoustic recorder.
For instance, the size and shape of the recording horn can be changed at the press
of a button.
The program is divided into three sections:-
[1] The Recording Horn
The partial differential equation governing the recording horn is turned into
N ordinary simultaneous differential equations by sectioning the horn into N parts
and matching the boundary conditions.
N can be varied at will, but it is found that N = 400 gives consistent results.
[2] The Air Cavity Between the Horn Mouth and Diaphragm
This cavity acts as an impedance changing transformer.
Signal transmission time across this cavity is not taken into account.
It is treated as a lumped element.
[3] The Mechanical Elements: Diaphragm and Stylus.
Some of the detail - such as the distributed nature of the damping or the non-linear
nature of the cutting force - is not included.
Note: I have not been able to find any photos or drawings of a late Edison recorder.
Much of the acoustic recording technology seems to have been regarded as a trade secret.
|
|
|
The response of the recorder to a step function of pressure at the mouth
horn is shown. |
The response of the recorder to a step function of pressure at the mouth
horn is shown. |
|
|
|
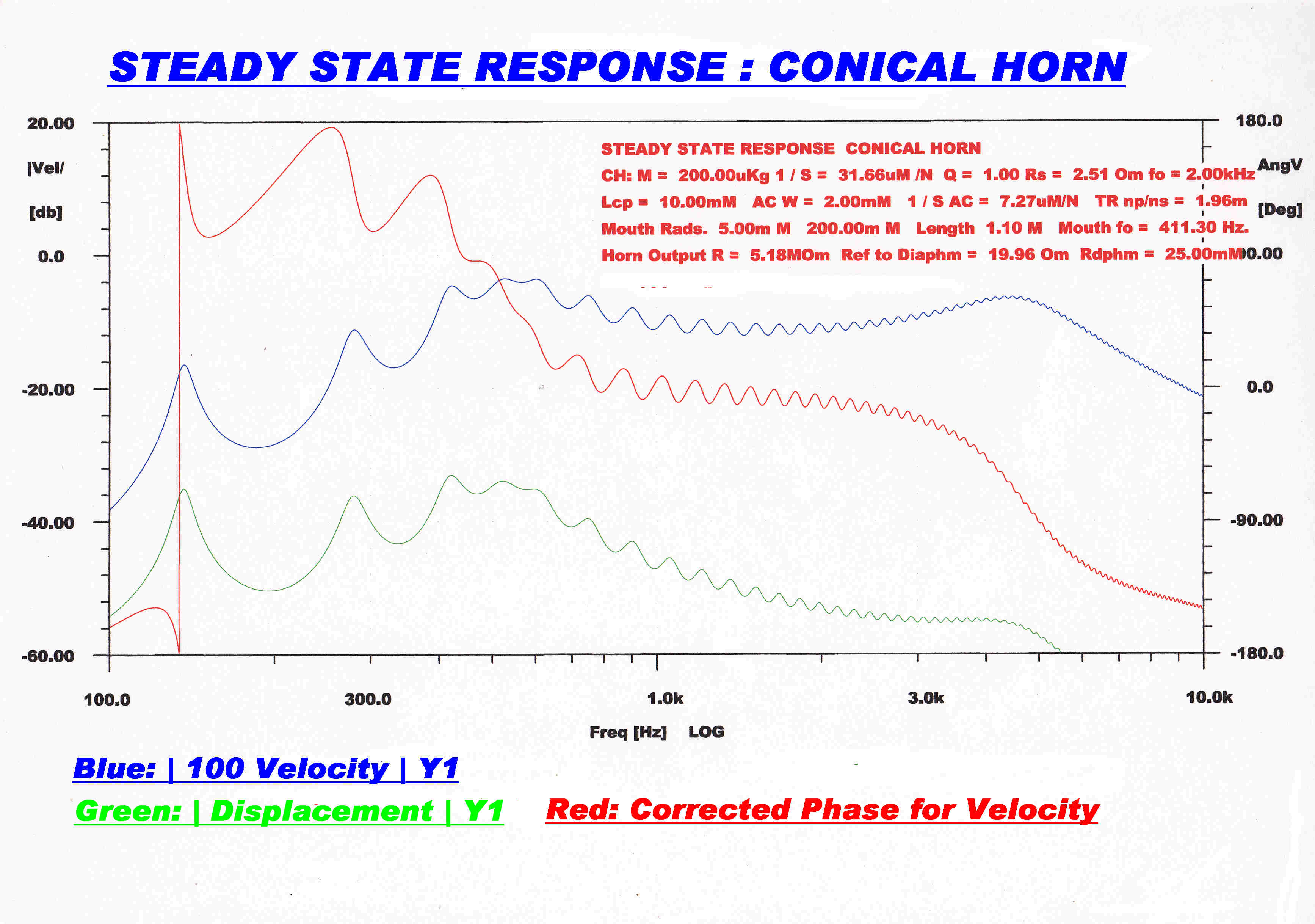
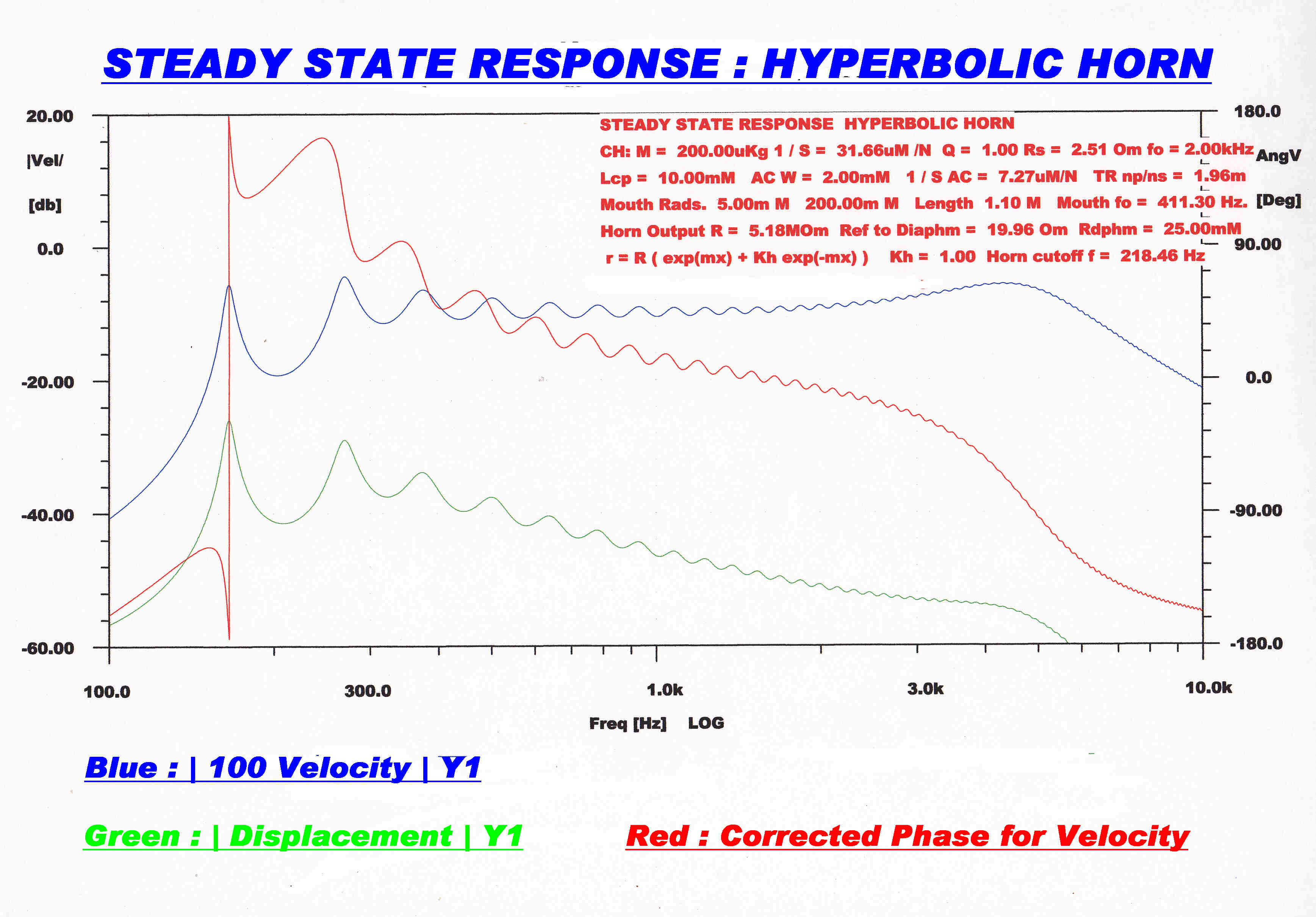
The response to a sinusoidal pressure wave of varying frequency at
the mouth of the horn is shown. |
The response to a sinusoidal pressure wave of varying frequency at
the mouth of the horn is shown. |
|
|
|
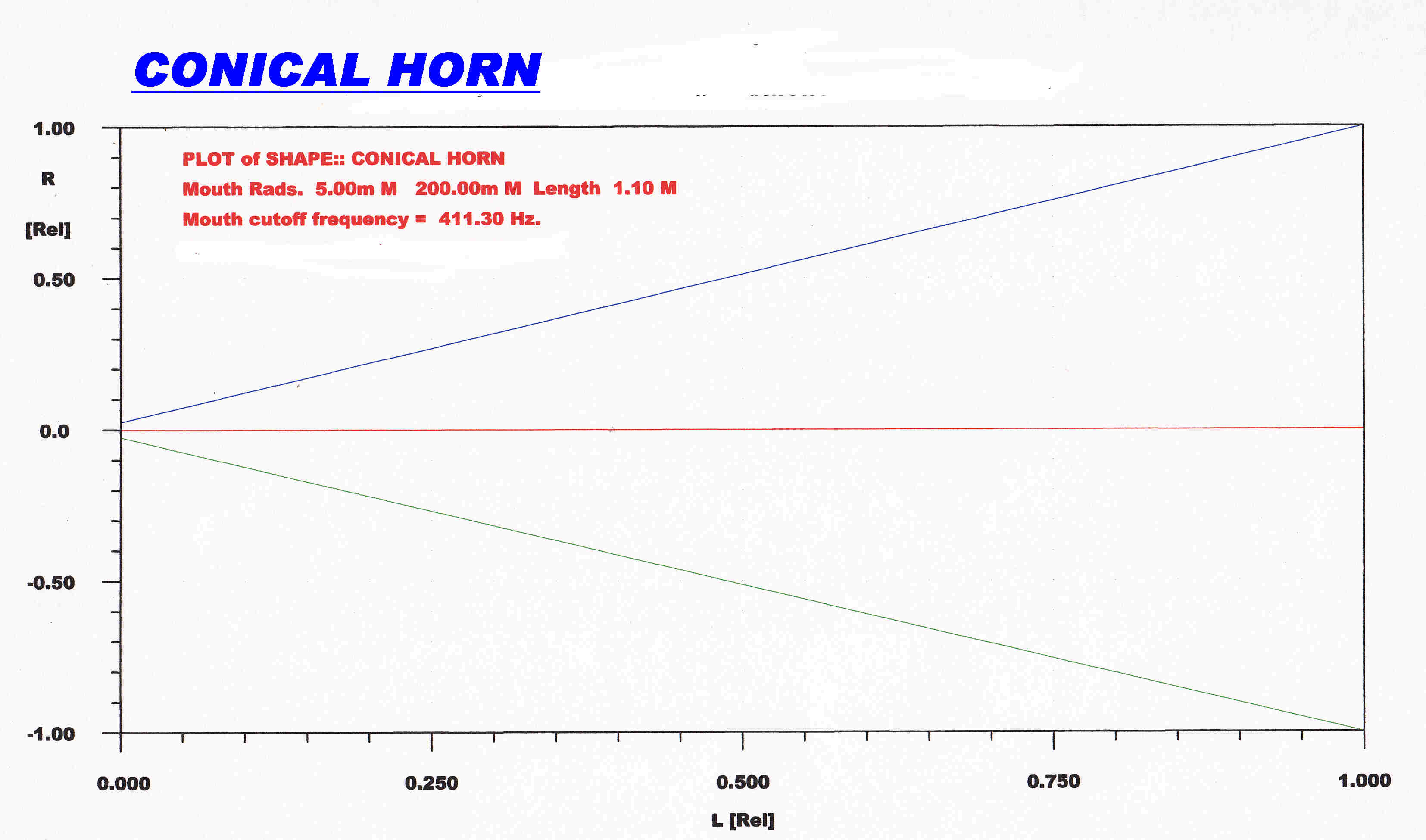
The shape of th conical horn used in the simulation is shown. |
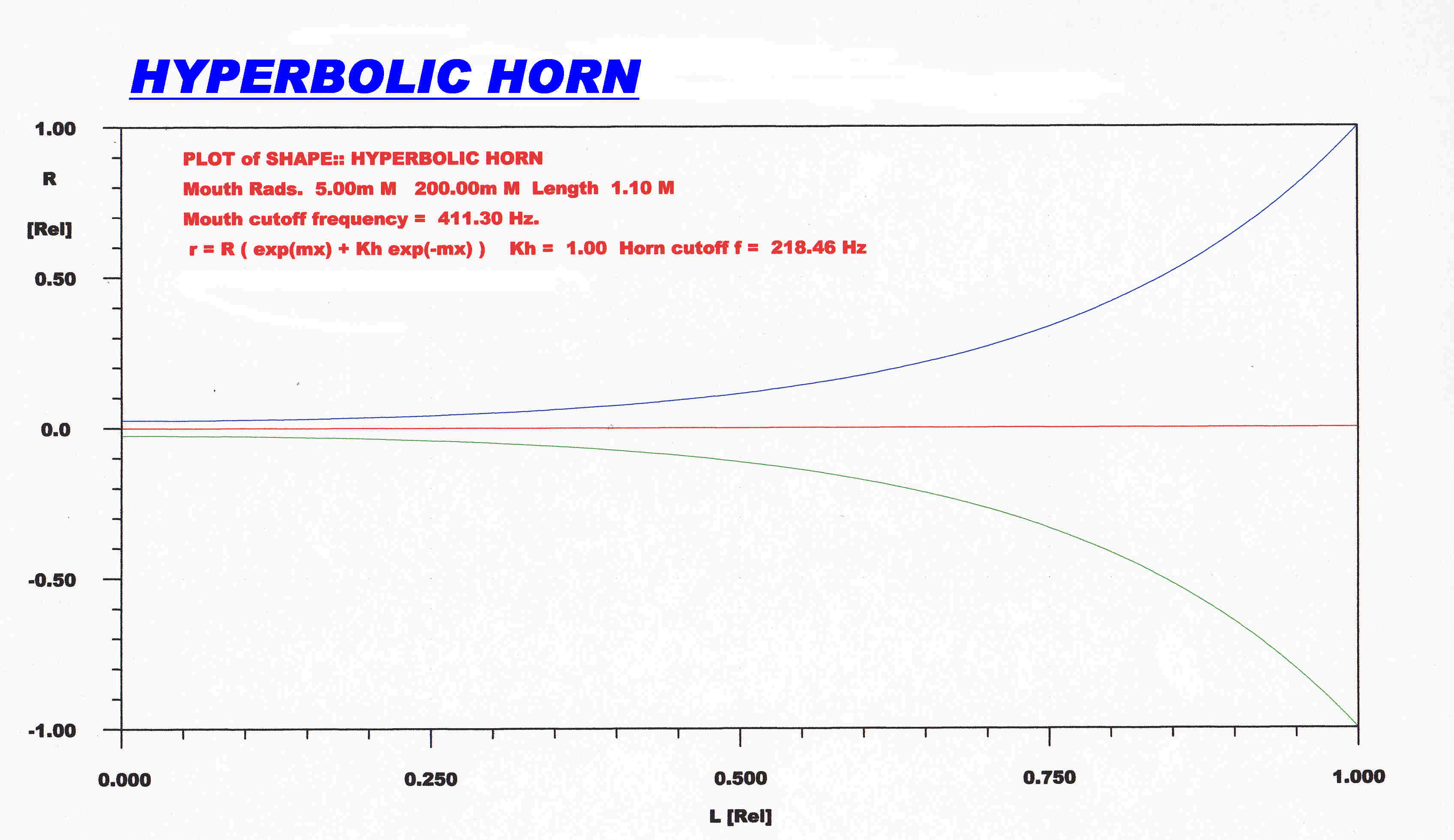
The shape of th hyperbolic horn used in the simulation is shown. |
The above computer simulation shows that the dynamic response of an acoustic recorder is largely determined
by the impedance mismatch between the horn and the mechanical cutting head.
This gives rise to reflections up and down the horn, peaks and troughs in the response and the characteristic
sound of mechanical recording.
With modern materials and computing methods it may be possible to design a mechanical cutting mechanism to give a much
better termination of the horn without limiting the sensitivity.
The response is then limited by that of the horn.
It is interesting to consider the response of the terminated horn.
Consider a horn with the following dimensions:-
Radius at narrow end: rs
Radius at large end: rt
Length: L
Distance along axis from narrow end: x
Radius of horn at distance x along horn: r
The conical horn is described by the equation:-
r = rs + (x/L)( rt- rs)
The exoonential and hyperbolic horn form is described by the quation:-
r = ( rs/( 1 + K ) )( eMx + Ke-Mx )
where K is a constant that determines whether hyperbolic or exponential.
K = 1 for hyperbolic: K= 0 for exponential.
We can now determine M by substituting the horn dimensions bsck into the equation:-
rt = (rs/( 1 + K ))( eML + e-ML )
Put eML = z
And M = ( 1/L) ln z
Then (rt/rs)( 1 + K ) = z + 1/z
Put (rt/rs)( 1 + K ) = q
0 = z2 - qz + K
z = (q/2){ 1 + [ 1 - 4K/q2 ]1/2 }
Substituting for q and z we get:-
M= ( 1/L )ln{ ( rt/2rs )( 1 + K ) + [ ( ( rt/2rs )( 1 + K ) )2 - K ]1/2 }
Conical , Exponential and Hyperbolic horns of the same dimensions are superimposed in the computer generated
graph below.
Note that the exponential and hyperbolic horns are very close.
The plot below shows the steady state response of the three horns used as radiators.
The small radius end is driven from a constant velocity sinusoid.
The pressure at the low radius input (green) gives a measure of the input impedance.
The pressure at the high radius mouth output (blue) gives the transfer function of the horn.
Because of reciprocity, these curves also apply to the horn as a receiver.
|
|
|
|
This shows that the response of the hyperbolic horn is close to ideal. |
The response of the exponential horn is very close to the hypersonic response. |
The response of the conical horn is far from ideal. |
PLAY BACK DETAILS
ACOUSTICS
Playback characteristic:
Constant velocity.
Signal Filtering:-
4th Order Maximally Flat Low Pass 6.5KHz.
4th Order maximally Flat High Pass 100Hz.
Stylus Diameter: 1 thou. Spherical.
Tracking Weight: 1.5 grams.
ELECTRICALS
Playback characteristic:
Constant velocity above 250Hz.
Constant Amplitude below 250Hz.
Signal Filtering:-
4th Order Maximally Flat Low Pass 8KHz.
4th Order maximally Flat High Pass 50Hz.
Stylus Diameter: 1 thou. Spherical.
Tracking Weight: 1.5 grams.
Note: The average depth of cut on an Edison acoustic disc seems to be about 0.8 thou.,
so the maximum displacement with modulation is +(-) 0.8 thou..
The maximum displacement on a 78 lateral is about +(-) 2 thou., so the output from
an Edison diamond disc is about 10 db down on a lateral.
An Edison acoustic reproducer is much easier on a disc than the lateral equivalent,
which also had the nasty habit of sheddig slivers of steel onto the track.
Nevertheless Edison discs did wear, and all the discs featured show signs of wear.
Some of the distortion on heavily cut transients is due to wear - not the recording
or reproducing equipment.
The discs have been played with a constant velocity playback characteristic and no further
equalisation has been used.
This gives a good idea of just how close the Edison discs come to the ideal acoustic curve.
Further equalisation between about 150 and 400 Hz. does add more "body" to the sound, but this
has not been used.
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[1] |
11,373 |
51900-L |
1927 |
Pretty Lips - Earl Oliver's Jazz Babies |
|
[2] |
11,372 |
51900-R |
1927 |
Where Do You Work-a John? - Earl Oliver's Jazz Babies |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[3] |
9770 |
51418-R |
1924-1925 |
Somebody Loves Me - Nathan Glantz and His Prchestra |
|
[4] |
9772 |
51418-L |
1924-1925 |
Tea for Two - Green Brothers' Novelty Band |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[5] |
7075 |
50661-L |
1920 |
Alice Blue Gown - Helen Clark |
|
[6] |
7077 |
50661-R |
1920 |
Irene - Helen Clark |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[7] |
8618 |
51089-R |
1922-1923 |
Lonesome Mama Blues - Fred Van Eps |
|
[8] |
8635 |
51089-L |
1922-1923 |
Frolic of The Coons - Fred Van Eps |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[9] |
10937 |
51745-R |
1926-1927 |
Chick, Chick, Chick, Chicken. - Earl Oliver's Jazz Babies. |
|
[10] |
10938 |
51745-L |
1926-1927 |
Show That Fellow The Door - Earl Oliver's Jazz Babies. |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[11] |
11178 |
51826-L |
1926-1927 |
Measley Blues - Joe Candullo and His Everglades Orchestra |
|
[12] |
11177 |
51826-R |
1926-1927 |
Bass Ale Blues - Joe Candullo and His Everglades Orchestra. |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[13] |
10759 |
51679-L |
1926-1927 |
Love Bound - Jack Stillman's Orchestra |
|
[14] |
10758 |
51679-R |
1926-1927 |
Dreaming of a Castle in The Air - Jack Stillman's Orchestra. |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[15] |
10293 |
51538-L |
1925-1926 |
On The Oregon Trail - Golden Gate Orchestra |
|
[16] |
10290 |
51538-R |
1925-1926 |
Little Peach - Jack Stillman's Orchestra |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[17] |
8929 |
51155-L |
1923-1924 |
King Tut - Billy Jones and Ernest Hare |
|
[18] |
8923 |
51155-R |
1923-1924 |
Barney Google - Billy Jones and Ernest Hare |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST |
|
[19] |
10565 |
51568-L |
1925-1926 |
The Old Grey Mare - Billy Jones and Ernest Hare |
|
[20] |
10505 |
51618-R |
1925-1926 |
How's Your Folks and My Folks - Billy Jones and Ernest Hare |
|
TRACK |
MATRIX |
CATALOG |
YEAR |
TITLE - ARTIST [ELECTRICAL RECORDING] |
|
[21] |
18314 |
52258-L |
1928-1929 |
That Wonderful Night and You - Jack Stillman's Orchestra |
|
[22] |
18313 |
52258-R |
1928-1929 |
Little Mother - Jack Stillman's Orchestra |
The telephone was invented in 1876.
In 1879 Edison patented a "loud speaking telephone".
This depended on a sensitive audio amplifier which could produce full acoustic
output for a very small electrical power input.
The operating input power was mechanical.
The technique was employed in a number of other devices described below.
The vacuum tube was not invented until 1906 and produced nothing usable
until at least 1910, so Edison's efforts are even more astounding.
OPERATING PRINCIPLE
Newly liberated hydrogen reduces the coefficient of friction between two surfaces.
This forms the basis of Edison's amplifier.
DESCRIPTION
A chalk wheel is saturated with sodium hydroxide and rotated at high speed.
A platinum strip, attached to the centre of a loud speaker diaphragm, is pressed
against the wheel, so friction produces a pull on the strip due to the rotation.
A DC current is passed through the wheel and onto the platinum strip.
Hydrogen is liberated at the chalk platinum interface by electrolysis.
This reduces the coefficient of friction and hence the in-line force on the strip.
Now if a small audio signal is added in with the DC bias, the force on the strip
will be modulated by it and an audio output from the speaker diaphragm will result.
Note that the power for the audio output comes from the rotational power input.
As the rotational speed of the chalk wheel is increased, the memory of "old"
hydrogen is removed more quickly, and so it is expected the speed of response to
an audio signal would be increased.
Various improvements were patented. For instance in 1880 a spring motor was added
to drive the chalk motor.
231,704 31 August 1880.
Edison used the high sensitivity of the chalk wheel amplifier to produce
a high gain repeater amplifier for long distance telephony.
340,707 27 April 1886
The audio output of the amplifier was coupled directly into another of his inventions
- the carbon microphone.
Although not known for its linearity or freedom from noise, this microphone was capable
of a large audio output.
Further patents were made to turn the amplifier into a two way system with the
use of hybrid coils.
422,579 4 March 1890
478,743 12 July 1892
Two way systems require a high degree of linearity, so the system would probably
have failed due to cross talk, but great thinking for 1892.
A drawing of an Edison electrical cutting head is shown above.
The large force available from the chalk wheel amplifier is used to drive the disc cutter.
The DC force applied to the cutting stylus must be well defined to standardise the
cut depth. The DC force from the chalk amplifier is, however, highly variable and must
not be passed on to the cutter.
In other words, the system must be AC coupled.
An air chamber placed between the two diaphragms provides the AC coupling.
A passage with a very small diameter equalises the atmospheric pressure with the air chamber.
It does not respond to the fast audio variations.
|
|
|
The cutting head was coupled to the telephone line through a transformer
and the recording cut into a wax cylinder. |
The screw thread drive for the head traversing mechanism is shown. |
Attempts were made to record sound for film with acoustic recorders.
The actors wandered away the recording horns, and the system was not
sensitive enough to pick up remote dialogue.
To correct this, it was proposed to use electrical recording.
The output from carbon microphones in the walls of the movie set was added (mixed) and the
composite signal applied to an electrical recorder.
An out of scale diagram explaining the action in a mechanical audio amplifier used
in some Edison cylinder phonographs is shown above.
It is believed that it was not an Edison invention, but, nevertheless, was widely used in Edison
cylinder phonographs to provide music for public functions.
The first example I saw in the fifties came from Government House in Queensland.
It was used to provide music at garden parties at the turn of the century.
The amplifier employs the capstan principle.
The tension on the output side of a capstan To is related to the
input tension T by the equation:-
To = e(μθ) T
where
To is the output force
T is the input force
μ is the coefficient of friction
θ is the wrap amgle
A band of low elasticity is wrapped around a turning capstan powered by the clockwork
motor of the phonograph.
One end drives the reproducer diaphragm. The other end is driven by a cantilever
perturbed by modulation on the vertical cut recording.
This results both in a variation of the input tension and and also the angle of wrap.
Because of the capstan equation, a very large variation of force is applied to the horn
loaded diaphragm.
Since both θ and T vary with the displacement x of the band, we have on
differentiating the above expression:-
dTo/dx = e(μθ) [ μ dθ/dx + dT/dx ]
Both dθ/dx and dT/dx can be calculated from the detail in how the band is
terminated, and so the gain of the amplifier.
From memory the quality was more than acceptable.